Delta xis

(créditos ao professor James e seu fantástico canal no Youtube, o qual utilizei para verificar as informações que estudei, antes de compilar para vocês)

Em um experimento aleatório sabemos os possíveis resultados, mas não qual resultado em particular ocorrerá. Temos a probabilidade de um evento: P(A). E esta probabilidade pode ser descrita assim: 0 <= P(A) <= 1

A interpretação dos resultados obtidos pode ser frequentista ou bayesiana. O primeiro considera o comportamento da probabilidade, caso testes infinitos fossem realizados, e o segundo interpreta a probabilidade como um grau subjetivo de crença. Basicamente, é a lei dos grandes números que vai gerar uma estimativa, a partir de quanto mais testes forem realizados, da verdadeira probabilidade. Então, note a natureza iterativa deste ramo da estatística. Não há respostas certas, apenas aproximações, estas sujeitas a uma das interpretações acima mencionadas.

Outro detalhe interessante é que, na estatística, fala-se muito em perda da memória. O apostador acha que os dados ou a roleta diante dele vai levar em conta que, depois de dezenas de apostas, o resultado que ele quer estará mais próximo de sair. Sinto informar, mas a sorte tem amnésia. O jogo do tigrinho não quer saber se você perdeu demais e precisa ganhar por causa de sua crença em a sorte estar chegando agora. E demonstro isso no próximo parágrafo.

É impossível falar do assunto sem usar moedas, e essa hora chegou. Se você lançar uma moeda dez vezes, e sair cara em todos os lançamentos, qual é a probabilidade de sair cara no próximo lançamento? A probabilidade permanece 50%. E por que seria diferente? Uma moeda possui apenas duas faces; não deixou de ter mais ou menos que isso com o tempo. Isso inclusive é conhecido como a falácia do apostador, ou lei da média.

O espaço amostral, ou seja, todos os possíveis resultados de um experimento, é representado de forma parecida com o observado na teoria de conjuntos. E um evento é um subconjunto do espaço amostral. Assim, o espaço amostral de um casal de dois filhos, por exemplo, fica assim: S = {MM, MF, FM, FF}. Lembre-se de observar a ordem dos eventos. Para representar um evento contendo um filho do sexo masculino e outro feminino, descrevemos assim: E = {MF, FM}. E como, no espaço amostral, todos os elementos têm a mesma chance de ocorrer, dizemos que são equiprováveis. P{MM} = 25% :::: P(E) = P(FM) + P(MF) = 50%

Cabe também fazer uma diferenciação: eventos podem ser disjuntos ou não disjuntos. Quando são disjuntos, não podem ocorrer ao mesmo tempo, como um dado sair os números 5 e 6 ao mesmo tempo, ou um time ganhar e perder uma partida de futebol ao mesmo tempo. Intersecção de A com B é igual a zero. Por sua vez, os eventos não disjuntos podem ocorrer simultaneamente, como dois voos partirem no mesmo horário ou uma pessoa ser formada em Economia e Letras. Intersecção de A com B é diferente de zero.

Pegando um baralho como exemplo (ignorem essas cores aleatórias dessa imagem e finjam que só preto e vermelho são usados), qual a chance de selecionarmos uma carta que seja rei ou 7? Temos um evento disjunto (só é possível somar as probabilidades por causa disso), e as cartas rei ou 7 somam 8. O total de cartas é 52, então a probabilidade é 8 / 52. Intuitivo. Se quiser usar notação, escreva: P(R)+P(7) = 4 / 52 + 4 / 52.

Agora, se quisermos verificar a probabilidade de tirar uma rainha ou qualquer carta vermelha, temos um evento não disjunto, ou seja, temos elementos que fazem parte do mesmo evento (rainha ou cartas vermelhas). Como dito acima, a intersecção de A com B é diferente de zero. Nesse caso, quais cartas participam da interseção? As rainhas vermelhas. E estas, por estarem na interseção, devem ser subtraídas. Com notação, fica assim:

P(R ou Verm) = P(R) + P(Verm) – P(R e Verm)➡️4 / 52 + 26 / 52 – 2 / 52 ➡️ 7 / 13

Os eventos complementares são eventos disjuntos que, ao se somar as probabilidades, o resultado dá 1. Isso ocorre não importa quantas vezes se lance uma moeda, por exemplo. Os espaços amostrais não possuem elementos em comum. A notação para eventos complementares é um C sobrescrito: A^c.

Para o exercício a seguir, vamos usar o cálculo da combinação porque a ordem dos elementos importa. O primeiro lugar é campeão da Copa do mundo e o segundo é vice. Ganha quem fizer mais gol. O código do cálculo está disponível em Latex. Abaixo, uma colinha, caso precise se recordar de como calcular combinação:

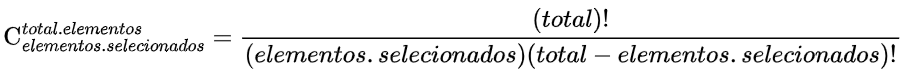
Exercício disponível no canal do Prof. James:

Um hospital possui 5 psiquiatras e 9 psicólogos em seu quadro e vai formar uma comissão de 5 profissionais. Se a seleção for feita aleatoriamente, qual a probabilidade de essa comissão ser formada por dois psiquiatras e três psicólogos?

\text{Espaço amostral:  }\mathrm{C}_{14}^{5} ::: \text{ Psiquiatras:  }\mathrm{C}_{5}^{2} ::: \text{Psicólogos:  }\mathrm{C}_{9}^{3} \newline \frac{\mathrm{C}_{5}^{2}\mathrm{C}_{9}^{3}}{\mathrm{C}_{14}^{5}}=\frac{60}{143}=0,4195

Para praticarmos um pouco, observando a proposta inicial do post, seguem abaixo as probabilidades de todas as mãos de pôquer. Mão de cinco cartas. Os cálculos de combinação são simbolizados assim: C (total, elementos selecionados). Ao final dos cálculos, deixei o código em Latex correspondente.

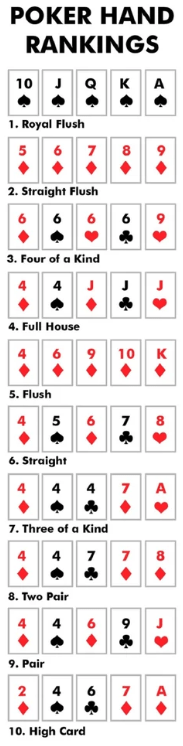
Royal Flush: 0,00000154 (0,000154%)
No pôquer, um royal flush é a mão mais rara e consiste em ás, rei, dama, valete e dez, todos do mesmo naipe. Como existem 4 naipes, cada um tem exatamente uma combinação de royal flush (A, K, Q, J, 10). Portanto, existem 4 combinações possíveis de royal flush, divididas pela quantidade de cartas: C(52, 5).

Então, a probabilidade de obter um royal flush em uma mão de cinco cartas é de aproximadamente 0,000154%, ou cerca de 1 em 649.740 mãos.

Straight flush: 0,00001385 (0,001385%)

Note que há um zero a menos do que o resultado do Royal flush. O cálculo, aliás, é semelhante ao do Royal flush, com uma diferença: existem 10 possíveis sequências de straight flush em cada naipe (A-2-3-4-5 até 10-J-Q-K-A, excluindo o royal flush). Existem 4 naipes, portanto, existem 10×4 = 40 combinações possíveis de straight flush.

Temos que subtrair as 4 combinações de royal flush já contadas anteriormente. 40−4=36. Em seguida, divida 36 por C(52, 5).

Four of a kind: 0,00024 (0,024%)

Número de combinações de “four of a kind”: Existem 13 valores possíveis (A, 2, 3, …, K) e em cada valor, há exatamente uma maneira de escolher as 4 cartas desse valor. A quinta carta deve ser de um valor diferente dos quatro, e há 48 opções restantes para essa quinta carta (pois 52 – 4 = 48). Então, o número total de combinações é: 13×48=624.

Temos eventos disjuntos aqui, então, por fim, divida tudo isso por 2.598.960, ou seja, C(52, 5).

Full house: 0,0014 (0,14%)
Baralho: C (52, 5); figura de trinca: C (13, 1); naipe de trinca: C (4, 3); figura de par: C (12, 1); naipe de par: C (4, 2)
(note que, em C (12, 1), uma figura de trinca já foi selecionada, então restam 12)
P = (C(13, 1) * C(4, 3) * C(12, 1) * C(4, 2)) / 2.598.960 = 0,0014

Flush: 0,00196 (0,196%)

Para calcular a probabilidade de obter um flush (cinco cartas do mesmo naipe, mas não em sequência) em uma mão de cinco cartas no pôquer, começamos calculando C(52, 5). Cada naipe tem 13 cartas, então para escolhermos 5 cartas de um único naipe, calculamos C(13, 5) = 1287. Existem 4 naipes, então o número total de combinações possíveis de flush é obtido multiplicando-se 1287 por 4.

Um straight flush (incluindo royal flush) é uma mão que é ao mesmo tempo um straight e um flush, então é preciso subtraí-los. Existem 40 straight flushes (incluindo os 4 royal flushes). Portanto, o número de flushes que não são straight flushes é: 5.148−40=5.108.

Por fim, divida 5108 por C(52, 5).

Straight: 0,0039 (0,39%)

Existem 10 possíveis sequências para um straight (A-2-3-4-5 até 10-J-Q-K-A). Para cada sequência, as 5 cartas podem estar em qualquer um dos 4 naipes, então o número de combinações para cada sequência é ( 4⁵ = 1.024 ). No entanto, essa contagem inclui também os straight flushes, que devem ser excluídos.

Existem 40 straight flushes (incluindo os 4 royal flushes), conforme calculado anteriormente. Número total de straights = 10 * 1.024 – 40 = 10.240 – 40 = 10.200

Por fim, divida 10.200 por C(52, 5)

Three of a kind: 0,0255 (2,55%)

Para obter o número a ser dividido por C(52, 5), multiplique os 13 valores possíveis (A, 2, 3, …, K) por C(4, 3), ou seja, 4 maneiras de escolher 3 das 4 cartas desse valor.
As duas cartas restantes devem ser de valores diferentes do valor da trinca e diferentes entre si. Existem 48 cartas restantes para a quarta carta e 44 cartas restantes para a quinta carta (após escolher a quarta carta), então multiplique por C(48, 2). Tudo isso resulta 58.656. Agora é só dividir por C(52, 5).

Two pair: 0,0475 (4,75%)

Existem 13 valores possíveis para o primeiro par e 12 valores possíveis para o segundo par. Para cada par, existem C(4, 2) = 6 formas de escolher duas das quatro cartas desse valor.
As duas cartas restantes devem ser de valores diferentes, então há 44 cartas restantes para a quinta carta (depois de escolher os dois pares).
Portanto, o número total de combinações de “two pair” é: C(13, 2) * C(4, 2) * C(4, 2) * C(44, 1), totalizando 123.552. Divida este valor por C(52, 5) e pronto.

Pair: 0,4426 (44,26%)

Existem 13 valores possíveis para o par. Para cada valor do par, existem C(4, 2) maneiras de escolher 2 das 4 cartas desse valor. As três cartas restantes devem ser de valores diferentes entre si e diferentes do valor do par. Existem 48 cartas restantes para a primeira das três cartas, 44 para a segunda, e 40 para a terceira. A conta fica assim:

C(13, 1) * C(4, 2) * C(48, 1) * C(44, 1) * C(40, 1) / 3! ➡️ 13 * 6 * 48 * 44 * 40 / 6 = 1.098.240

Por fim, divida o número acima por C(52, 5).

High card: 0,5012 (50,12%)

Parece ser a mais simples das contas, mas as aparências enganam. Para calcular a probabilidade, vamos levar em conta que uma mão de high card não deve conter nenhum par, two pair, three of a kind, straight, flush, full house, four of a kind, ou straight flush. Pegue os valores dos cálculos anteriores e some tudo. As combinações que não são high card são:

• One pair: 1.098.240 combinações
• Two pair: 123.552 combinações
• Three of a kind: 54.912 combinações (corrigido a partir do cálculo anterior)
• Straight: 10.200 combinações
• Flush: 5.108 combinações
• Full house: 3.744 combinações
• Four of a kind: 624 combinações
• Straight flush: 40 combinações (incluindo royal flush)

A soma dessas combinações é igual a 1.296.420. Agora, subtraia C(52, 5) por esse número. Resultado 1.302.540.

Por último divida este valor por C(52, 5).

\text{Royal flush: } \frac{4}{\binom{52}{5}}=0,000001539 \newline
\text{Straight flush: } \frac{36}{\binom{52}{5}}=0,000013851 \newline
\text{Four of a kind: } \frac{624}{\binom{52}{5}}=0,00024 \newline
\text{Full house: } \frac{\binom{13}{1}\binom{4}{3}\binom{12}{1}\binom{4}{2}}{\binom{52}{5}}=0,0014\newline
\text{Flush: } \frac{5108}{\binom{52}{5}}=0,00196\newline
\text{Straight: } \frac{10200}{\binom{52}{5}}=0,0039 \newline
\text{Three of a kind: }13*\binom{4}{3}*\binom{48}{2}=58.656 \to \frac{58656}{\binom{52}{3}}=0,0225
\text{Two pair:  }\binom{13}{2}*\binom{4}{2}*\binom{4}{2}*\binom{44}{1}=123.552 \to \frac{123552}{\binom{52}{3}}=0,0475 \newline
\text{Pair: } \frac{\binom{13}{1}*\binom{4}{2}*\binom{48}{1}*\binom{44}{1}*\binom{40}{1}}{3!}=1.098.240 \to \frac{1.098.240}{\binom{52}{5}}=0,4426 \newline
\text{High card: }\newline \binom{52}{5}-1.098.240+123.552+54.192+10.200+5.108+3.744+624+40\newline =2.598.960-1.296.420=1.302.540 \newline \frac{1.302.540}{\binom{52}{5}}=0,5012