Delta xis

A geometria é o ramo da matemática que mais lembra o ofício de um delegado: antes de qualquer cálculo, você precisa sempre investigar o que o enunciado não dá logo de cara. Entre relações trigonométricas e razões, tem sempre coisa que o polígono diante de você revela. Várias delas aprendi com o canal PreMath, que recomendo, e que comprova a teoria que já li internet afora de que, quando se quer encontrar uma explicação fácil para algo, pesquise um indiano explicando.

Espiral de Teodoro

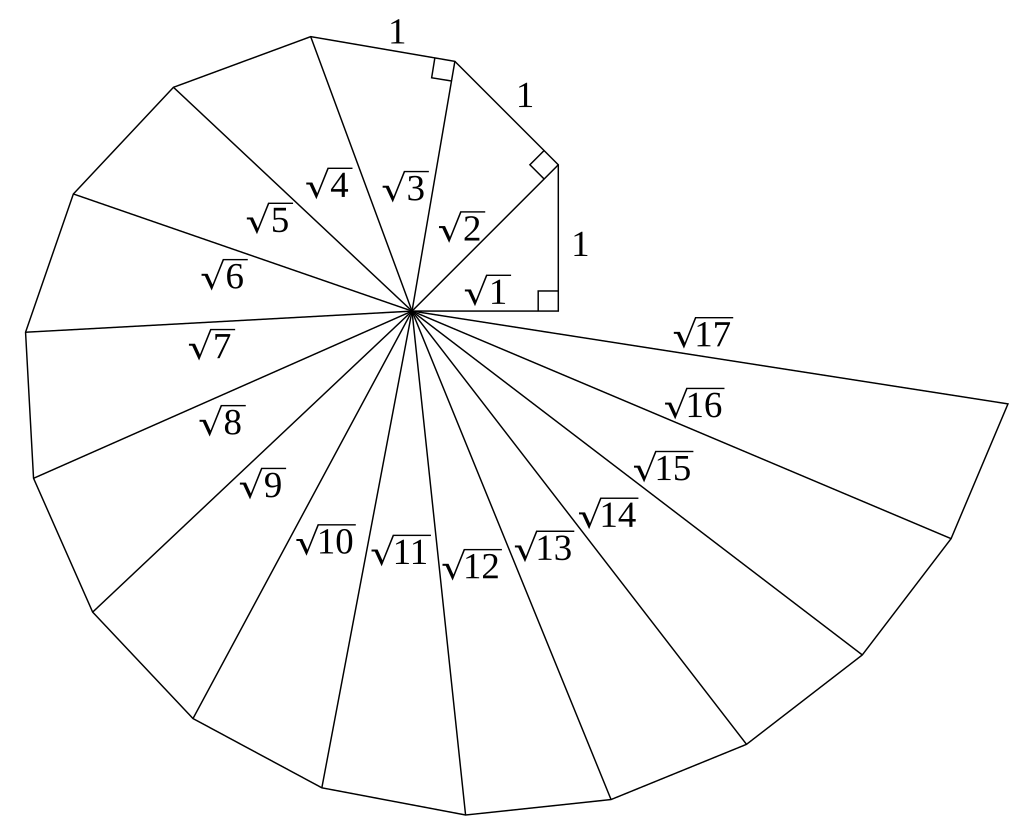
Consiste em uma espiral infinita, formada por triângulos, cujo padrão consiste em a base n do triângulo ser uma raiz, a altura ser 1, e a hipotenusa ser uma raiz n + 1. Prático, né?

Triângulo especial

Um triângulo retângulo especial possui alguma característica regular que facilita cálculos. Por exemplo, um triângulo retângulo pode ter ângulos formando relações características, como 45°–45°–90°, ou seja, um triângulo retângulo “baseado em ângulo”. Um triângulo retângulo “baseado em lado” tem lados com comprimentos formando relações de números inteiros, como 3 : 4 : 5, ou de outros números especiais, como a proporção áurea [1].

E aqui quero chamar sua atenção para os triângulos de proporção 3 : 4 : 5, pois são comuns em exercícios do Ensino Médio. Mesmo tendo apenas uma medida fornecida pelo exercício, você consegue obter todos os outros lados. Os triângulos 3 : 4 : 5 são os únicos com lados em progressão aritmética. Triângulos baseados sobre triplas pitagóricas são heronianos: têm áreas, bem como lados, inteiros.

Veja abaixo como descobrir todos os lados de um triângulo retângulo tendo apenas uma medida:

• Lado 10: os outros lados são 6 e 8 (3, 4 e 5 vezes 2);
• Lado 16: os outros lados são 12 e 20 (3, 4 e 5 vezes 4);
• Lado 21: os outros lados são 28 e 35 (3, 4 e 5 vezes 7).

Existem diversas triplas pitagóricas bem conhecidas, incluindo aquelas com lados nas relações:

3: 4 :5
5: 12 :13
8: 15 :17
7: 24 :25
9: 40 :41

Interpolação

E se estivermos diante de um polígono com mais de 4 lados? Aí a gente aplica um conceito da progressão aritmética, resumido na concisa fórmula abaixo:

a_n = a₁ + (n – 1) * r

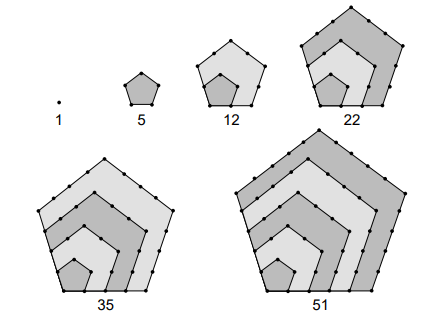
Bônus: em questão do ENEM, já foi cobrado o número pentagonal. A questão pergunta qual é o oitavo número pentagonal. E a imagem, embora interessante, mais confunde do que explica. Talvez apenas apresentando números ficasse mais fácil de responder. O número pentagonal é uma progressão aritmética: você começa com um número n, o número 1. Para obter o próximo número, você soma esse n com n mais 1. Para as próximas somas, você soma o resultado da soma anterior por n da soma anterior mais 3. Veja exemplos abaixo:

1
1 + 4 = 5
5 + 7 = 12
12 + 10 = 22
22 + 13 = 35

Mais pistas

Outras pistas valiosas estão diante de nosso nariz. A altura do triângulo não pode ser maior do que metade da base deste. Caso o exercício possua muitas linhas, não se desespere e lembre-se do teorema de Tales: se cortarmos duas retas por várias retas paralelas, os segmentos em ambas são proporcionais. Se observarmos bem, tem sempre uma proporção disponível para nos guiar.

Quanto aos círculos, o teorema de Tales afirma também que se uma reta AC é o diâmetro desta circunferência, então os pontos ABC formam um triângulo retângulo.

Atalhos

E se acha que exagero quando afirmo que geometria tem mais a ver com investigação do que com cálculos, peguei um exercício do PreMath para mostrar a vocês que, sabendo certas coisas, é possível ganhar muito tempo. Aqui, precisamos descobrir a área da parte rosa, e para isso precisamos calcular o raio, a área do retângulo, do quarto de círculo e, por fim, subtrair a área do círculo pela do retângulo.

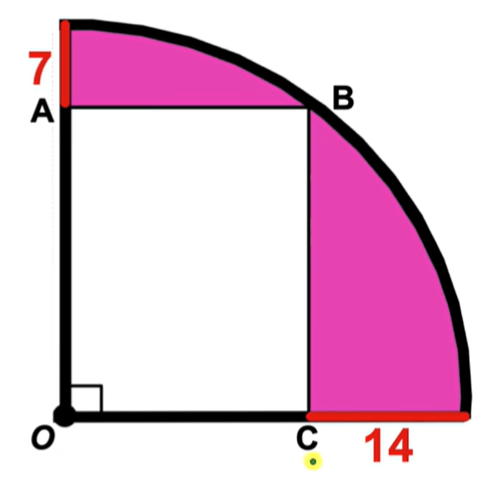
No vídeo, a resolução do exercício começa reunindo informações para se descobrir o raio do quarto de círculo. Isso é feito representando-se a diferença entre o raio e os números disponíveis no exercício. Assim, o lado AO do retângulo é r – 7 e o lado OC é r – 14. Em seguida, uma linha diagonal é traçada dentro do retângulo, de O até B. Esta linha é o raio. E como descobri-lo?

O vídeo propõe usar o teorema de Pitágoras para isso. Seguem os cálculos abaixo, precedidos do Latex correspondente.

a^2+b^2=c^2 \newline
(r-7)^2+(r-14)^2=r^2 \to \color{Red} r^2\color{Black} -14r+49+r^2-28r+196=\color{Red} r^2 \newline
-14r+49+r^2-28r+196=0 \to r^2-42r+245=0 \newline
\text{fatorando 245 >> 7 * 35, temos: }(r-7)(r-35) \newline
r-7 \Rightarrow r=7 \text{ ... }r-35 \Rightarrow r=35 \newline

Legal. Nessa etapa do exercício, descobrimos o raio e ficou fácil descobrir a área do retângulo, mas tem um detalhe. Nada disso seria necessário se a gente observasse que o triângulo cuja hipotenusa foi calculado é um triângulo especial. As dimensões do triângulo são 21, 28 e 35, certo? Esta é a proporção 3 : 4 : 5 mencionada agora há pouco. Basta multiplicar por 7. Note que a observação aqui é mais importante do que o cálculo em si. Enfim, assista ao resto do vídeo para acompanhar a resolução do exercício.