


Mais uma coisa que não ensinam nas escolas. Em vez de usar a dita fórmula de Bhaskara (que só é chamada assim aqui, mais uma jabuticaba nossa), porque não usar a de Viète? Vamos a ela.
Diante de um polinômio, comece substituindo xis por x = u + v. Em seguida, expanda o produto notável. Assim:
x2 – 8x – 9 = 0 👉 (u + v)2 – 8(u + v) – 9 = 0
u2 + 2uv + v2 – 8u – 8v – 9 = 0 👉👉 v2 + 2uv – 8v + u2 – 8u – 9 = 0
Repare que a parte em negrito é o mesmo polinômio com o qual começamos, então pode ser zerado mais à frente. Em seguida, vamos colocar o resto da equação em evidência. Com esse processo, vamos encontrar o valor de u e v será a única incógnita. Por fim, deixamos a variável ao quadrado de um lado e o número 25 de outro. Tiramos a raiz de 25 e, assim como faríamos em Bhaskara (fórmula quadrática), usamos o sinal ± ao final.
v2 + v (2u – 8) + u2 – 8u – 9 = 0 👉👉2u – 8 👉👉u = 4
v2 + v (2(4) – 8) + u2 – 8u – 9 = 0 👉👉v2 + v (8 – 8) + u2 – 8u – 9 = 0 👉👉
v2 +42 – 8(4) – 9 = 0 👉👉 v2 = 25 👉v = ±5
Por último, some o valor de u ao de v e obtenha dois resultados possíveis. Cabe a você aceitar ou rejeitar um dos resultados, de acordo com o que o exercício pedir.
x = u + v 👉👉x = 4 + 5 = 9 🎈🎈x = 4 + (-5) = – 1 🎈🎈 x = {-1, 9}
Bônus: mais uma forma de fatorar. Se o primeiro termo não estiver apenas com a variável ao quadrado, multiplique o último termo por este coeficiente. Em seguida, encontre números que, somando, tenham como resultado o segundo termo, e que, multiplicando, tenham como resultado o terceiro termo. Com o tempo, isso fica intuitivo, mas enquanto não se adquire prática, decomponha o número até encontrar os números menores que você precisa para satisfazer esta condição. Assim:
10x2 + 9x – 9 👉👉 x2 + 9x – 90
90 / 2👉 45 / 3 👉 15 / 3 👉5 / 5 👉 1
(2)(3)(3)(15) 👉👉 a + b = 9 👉👉 15 + (-6) = 9 👉👉 (x – 6) (x + 15)
Só isso? Na verdade, só falta uma coisa. Lembra do coeficiente que estava elevado ao quadrado? Vamos recolocá-lo na expressão acima, e simplificar.
(10x – 6) (10x + 15) ➗➗ (5x – 3) (2x + 3)
Além desses dois métodos, tem ainda o tic-tac-toe rule, que você pode conferir neste vídeo curtinho do canal Blue pen red pen. É basicamente uma variação desse método que acabei de mostrar acima, então fique à vontade para escolher o método com o qual você se adaptar melhor.
Discorrer sobre um tema atual pode nos fazer enxergar apenas o status quo, sem levar em conta o que já foi conquistado, a má vontade dos espaços de poder de antes. Essa semana estava folheando umas publicações antigas do sótão da casa de meus pais, e me deparei com esse almanaque dos anos 1990, publicado pela Istoé, com 1000 pessoas que colaboraram para o cinema ao longo do século XX. As imagens a seguir poderiam se confundir facilmente com as de um arquivo público, talvez de revistas do século passado, mas são apenas de 1996. Menos de 30 anos atrás. Às mulheres que estiverem lendo este post, mantenham um saquinho de vômito ao lado: não digam que não avisei…










Reúno aqui uma série de dicas para se ganhar vocabulário que dou nas aulas de inglês que ministrei ou ministro ao longo do tempo.
Advérbio que indica que algo é bastante, suficiente. Pode também ser usado em conversas, mais informalmente, para a pessoa informar a seu ouvinte que ela não vai mais tolerar certa situação. Uma curiosidade desse advérbio é que a posição dele é definida pela palavra que vem junto a ele. Se for um adjetivo, vem depois deste; se for substantivo, vem antes deste. He is not strong enough to lift all this weight. There are not enough chairs for the party. Fique atento também às locuções: soon enough (bem antes), fair enough (justo), enough said (já disse o bastante), enough is enough (já chega!), have had enough (estar cansado, já ter aguentado o bastante)… confira o dicionário para ver mais opções.
Muitas formas de se falar de lembranças em inglês. Reminisce é mais introspectiva, consistindo em rememorar, se relembrar de algo por conta próprio, geralmente movido por nostalgia. Remember, diferente do português, não é um verbo reflexivo, então nem sempre será encontrado acompanhado de um object pronoun. Possui também o sentido de celebrar, comemorar algo. Já remind é quando algo ou alguém (um terceiro, enfim) te faz lembrar de algo. Geralmente usado para compromissos: Remind me I need to buy more milk. Todos são verbos regulares.
Clássicos false friends. Intend informa ao ouvinte a intenção de se fazer algo, e pretend é quando se simula, finge uma situação. Ambos são verbos regulares.
Esta palavra é um non-count noun, sabia? Os falantes nativos não consideram conselhos como coisas contáveis. Ponto de vista interessante, com implicações (quase) filosóficas. Faz sentido, de certo modo: uma conversa pode trazer vários conselhos, ou nenhum, e às vezes a pessoa falando sequer se dá conta de que o que está falando pode se tratar de um conselho. Quem nunca observou, nos filmes ou nas séries, um personagem tendo um insight, um momento de autodescoberta, em que ele começa a contar a alguém sobre algo que aconteceu a um amigo, mas ele vai se envolvendo emocionalmente com tanto afinco no relato dele, que logo o ouvinte percebe que a pessoa está é falando dela própria. Então, vejam que interessante: um conselho pode partir até de nós para nós mesmos, então parece algo bem abstrato, difuso e difícil de contar, mesmo.
Exemplos de nominalização. Em excesso, pode deixar um texto prolixo. Use com moderação. O inglês não é muito dado a eles, então não espere encontrá-los com tanta frequência quanto o português: dar uma olhada (=olhar); dar uma verificada (=verificar)
Peço licença para trazer rapidamente a definição desta palavra, de acordo com o dicio.
s. fem.[Linguística] Operação que consiste em transformar uma oração em sintagma nominal para sua inserção numa frase matriz. Fórmula: O11+O2 = O. Ex: O1 – o herói chegou; O2 – isto causou alegria; O – a chegada do herói causou alegria. O princípio geral da nominalização é o mesmo, mas os meios morfológicos usados são vários.
Nominalização afixal: utiliza um afixo mais a raiz verbal. Ex: O governo constrói estradas. A construção de estradas.
N. infinitiva: utiliza afixo zero mais o infinitivo do verbo. Ex: O governo constrói estradas. Construir estradas.
N. simples: a que opera apenas com os sintagmas nominais da frase nuclear. Ex: O jardim tem flores. As flores do jardim. Também se chama nominalização a aplicação de um funcional (chamado nominalizador; p. ex., ‘que’) a uma frase para torná-la apta a funcionar como sintagma nominal ou parte dele numa frase complexa. Ex: Disse a verdade (frase simples; a verdade = sintagma nominal). Disse que era verdade (frase complexa; que era verdade = SN).
Já faz um tempo que encontrei esta questão, neste vídeo aqui, bem modesto, que desafia o estudante a encontrar padrões bem diante de seus olhos. Embora seja parecido com um exercício que apresentei aqui esse mês, aqui não temos a oportunidade de encontrar o valor de duas variáveis combinadas. Na verdade, em certa parte do exercício, em meio às suas pegadinhas, somos levados a um beco sem saída. Do qual só é possível se safar isolando-se os poucos números restantes e, novamente, fatorando-se uma última vez. Basicamente, é uma questão sem caminho definido, que o próprio estudante deve criar. Coisas fundamentais não são dadas pelo enunciado.
(x2+1)(y2+1)+9=6(x+y) /// encontre x2+y2
Spoiler alert: cuidado com o finalzinho da questão. x2+y2 NÃO É a mesma coisa que (x+y)2. Use e abuse das manipulações algébricas. Duas diferenças de quadrados, entre elas uma bem atípica, podem ser formadas, mas você terá de trazer algo ao exercício para conseguir isso. Pensar fora da caixa é fundamental aqui.
Confira a resolução abaixo em Latex:
(x^2+1)(y^2+1)+9=6(x+y) \newline
x^2y^2+x^2+y^2+1+9=6(x+y) \to x^2y^2\color{Red} +2xy-2xy\color{Black} +x^2+y^2+9+1-6(x+y)=0 \newline
\text{difference of squares: } (x+y)^2=x^2\color{Red} +2xy\color{Black} +y^2 \newline
\text{difference of squares: } (xy-1)^2=x^2y^2\color{Red} -2xy\color{Black } +1 \newline
(x+y)^2(xy-1)^2+9-6(x+y) \to \color{Blue} (x+y)^2(xy-1)^2+3^2-6(x+y)=0 \newline
\text{another difference of squares: } (\color{Blue} (x+y)\color{Black} -3)^2=(x+y)^2-6(x+y)+9 \newline
(xy-1)^2+((x+y)-3)^2=0\newline
\text{both polynoms must be zero, so...} \newline
xy-1=0 \to xy=1 \text{ and } (x+y)-3=0 \to x+y=3 \newline
\text{substitute in any of the polynoms:} \newline
(x+y)^2=x^2+2xy+y^2 \newline x^2+y^2=(x+y)^2-2(1) \to (3)^2-2=7Esta é daquelas coisas interessantes que nunca nos ensinam na escola. Pega a visão.

Como resolver isso aqui? Sabemos que um fatorial (um ponto de exclamação) é a multiplicação de um número por todos os seus termos anteriores até 1. E fatoriais duplos, triplos? Estes simplesmente são a multiplicação de um número por seus termos anteriores, com um intervalo maior entre eles. Veja a lista abaixo:
7! = (7)(7-1)(7-2)(7-3)(7-4)(7-5)(7-6) ou (7)(6)(5)(4)(3)(2)(1) = 5040
7!! = (7)(7-2)(7-4)(7-6) = 105
7!!! = (7)(7-3)(7-6) = 28
Antes de resolvermos o exercício, uma ressalva: (3!)! não é a mesma coisa que 3!!. Na verdade, aqui resolvemos o que está dentro do parênteses, e só depois usamos o ponto de exclamação externo, então temos: 3! = 6. Aplicando o ponto de exclamação externo a esse 6, temos 6! = 720.
Substituindo tudo, temos o resultado abaixo. Tente fazer primeiro, e depois confira a resposta colando o código em um editor Latex.
\frac{880*720}{5040*384}=\frac{55}{168}Acho que uma boa metáfora para entender como usar este conhecimento é a famosa dança das cadeiras, comum entre as crianças. Quando a música para de tocar, uma criança sempre fica de fora por vez, então começamos com 5!. Se quisermos que uma criança sempre fique de fora a cada duas vezes que a música para, usamos 5!!. A cada três vezes, 5!!!. Então, as probabilidades das crianças sentadas são: 5!=120; 5!!=15; 5!!!=10; 5!!!! e 5!!!!!=5.
Para quem gosta de reality shows, as especulações sobre quem vai ganhar o prêmio da atração ao passar três meses sem trabalhar podem ser feitas assim: se temos 12 participantes, temos…
12! = 479.001.600; 12!! = 46.080; 12!!! = 1944; 12!!!! = 384; 12!!!!! = 168; 12!!!!!! = 72.
Em primeiro lugar, o mundo maravilhoso da Internet nos poupa dessa tarefa de equlibrar pratos com sites abençoados como esse. Mesmo assim, decidi trazer o resultado de uma consulta para comentar com vocês. Nem todas as informações disponíveis podem parecer intuitivas à primeira vista, e como eu sou das humanas, preciso de tudo mastigadinho. Pense no balanceamento como um sistema linear, creio que isso pode ajudar. Ao passo que queremos isolar variáveis na matemática, como amiúde fazemos em várias ocasiões, na química queremos que os dois lados da fórmula, os reagentes e os produtos, tenham o mesmo número de átomos. Uma balança, pense sempre em uma balança, ao fazer esse processo. ⚖️
O site propõe dois métodos de balanceamento, e farei rápidos comentários (em azul) sobre possíveis dificuldades semelhantes às minhas:
| Balanceamento passo a passo usando o método de inspeção |
|---|
| Vamos equilibrar esta equação usando o método de inspeção. Primeiro, definimos todos os coeficientes como 1: 1 C4H10 + 1 O2 = 1 CO2 + 1 H2O Para cada elemento, verificamos se o número de átomos está equilibrado em ambos os lados da equação. C não está equilibrado: 4 átomos em reagentes e 1 átomos em produtos. Para equilibrar C em ambos os lados, nós: Multiplique o coeficiente de CO2 por 4 1 C4H10 + 1 O2 = 4 CO2 + 1 H2O H não está equilibrado: 10 átomos em reagentes e 2 átomos em produtos. Para equilibrar H em ambos os lados, nós: Multiplique o coeficiente de H2O por 5 1 C4H10 + 1 O2 = 4 CO2 + 5 H2O O não está equilibrado: 2 átomos em reagentes e 13 átomos em produtos. Para equilibrar O em ambos os lados, nós: Multiplique o coeficiente de O2 por 13 Multiplique o(s) coeficiente(s) de CO2, H2O, C4H10 por 2 2 C4H10 + 13 O2 = 8 CO2 + 10 H2O Esta parte me confundiu um pouco. De onde saíram esses 13 átomos em produtos? Então… quando multiplicamos CO2 por 4, temos 8 átomos de O. E quando multiplicamos H2O por 5, temos 5 átomos de oxigênio. Tudo isso do lado do produto. Para o reagente ficar com quantia igual de oxigênio, só resta multiplicar o coeficiente por 13.. Para não se confundir, ignore o número subescrito depois de O. C está equilibrado: 8 átomos em reagentes e 8 átomos em produtos. H está equilibrado: 20 átomos em reagentes e 20 átomos em produtos. Todos os átomos estão balanceados e a equação toda está completamente balanceada: 2 C4H10 + 13 O2 = 8 CO2 + 10 H2O |
C: a*4 = c*1
H: a*10 = d*2
O: b*2 = c*2+d*1
Atribua a = 1 e resolva a equação linear. 👇👇👇
a=1
C: 4 = c 👉c = 4
H: 10 = 2d 👉d = 5
O: 2b = 4*2 + 5*1 👉2b = 13 👉b = 6,5
Para chegar aos coeficientes inteiros, multiplique todos os resultados por 2. Os átomos não costumam trabalhar com números quebrados.
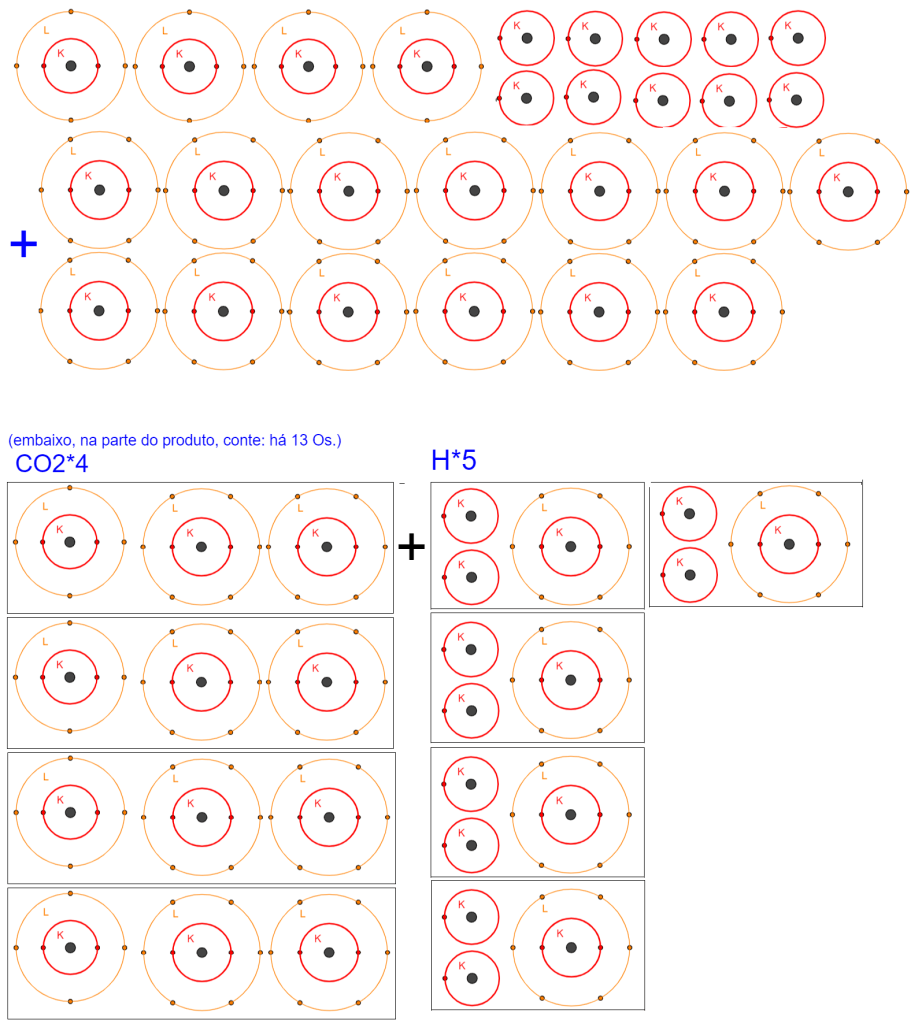
Por fim, despeço-me com uma demonstração visual de como um balanceamento funciona. Essa representação gráfica dos átomos foi obtida pelo Geogebra, com este material feito pelo brasuca Ricardo de Oliveira Peixoto.

Volta e meia circulam por canais de matemática algumas questões virais que exigem muito pensamento lateral para serem resolvidas. Algumas não passam de gente vaidosa querendo assustar com fórmulas prolixas, mas outras consistem em manipulações que nos demonstram que temos mais informações do que pensamos, ao ler um enunciado. A questão abaixo é uma dessas.
Se a+b=1 e a2+b2=2, quanto vale a11+b11?
A resposta está abaixo, em código Latex. Copie e cole em qualquer leitor para verificar. Mas antes disso, quero comentar algumas coisas. A maioria dos estudantes tem dificuldade de visualizar que uma razão, não importa os números usados, é sempre a mesma. 3 / 4 é a mesma coisa que (3 / 4)2 ou 9 / 12. E isso também ocorre com polinômios. Posso não saber os valores envolvidos nas variáveis, mas sei que a proporção permanece. Além disso, elevar uma operação ao quadrado tem a vantagem de dividir a razão em partes menores. E, quando menos se esperar, será possível encontrar algumas pistas. Então, o primeiro passo é esse: eleve a+b ao quadrado e fatore. Vamos encontrar a2+b2, mas também encontramos 2ab. Temos novidade aqui. Mantemos a e b ao quadrado no mesmo lugar e transferimos para o outro lado da igualdade esse número 2. E pronto, temos um valor estabelecido para ab.
Esse valor pode ser usado em todos os polinômios que você vai fatorar. Não importa a combinação que você obtiver, sempre será possível isolar ab, mesmo que você tenha que elevar a alguma potência. Não importa a potência, basta deixar ab entre parênteses e você consegue sempre usar esse valor. E o processo, com os próximos polinômios, é o mesmo: você mantém a+b elevado a alguma potência, e passa o valor obtido pela substituição de ab para o outro lado do sinal de igual. É matemática discreta, mas em alguns aspectos, é quase iterativa.
À medida que você descobrir valores para cada polinômio, você pode ir multiplicando um pelo outro e isolar ab sempre que possível. Vai chegar um momento em que a multiplicação das potências dos polinômios vai dar 11. E aqui a mágica acontece: você encontra a resposta apenas isolando, isolando e isolando.
Confira abaixo a resposta em Latex:
\text{Se }a+b=1 \text{ e } a^2+b^2=2 \text{ encontre valor de }a^{11}+b^{11} \newline
(a+b)^2=1^2 \to a^2+2ab+b^2 \to a^2+b^2+2ab=1 \newline 2+2ab=1 \to 2ab=-1 \cdots \color{Blue} ab=-\frac{1}{2} \newline
\color{Blue} (a+b)^3=1^3 \to a^3+3a^2b+3ab^2+b^3=1 \color{Black} \to a^3+b^3+3(ab)(a+b)=1 \newline
a^3+b^3+3(-\frac{1}{2})(1)=1 \to ...(-\frac{3}{2}) \to \color{Blue} a^3+b^3=1+\frac{3}{2}=\frac{5}{2} \newline
\color{Blue} (a^2+b^2)(a^3+b^3)=2\frac{5}{2} \color{Black} \to a^5+a^2b^3+a^3b^2+b^5=5 \to a^5+b^5+a^2b^2(a+b)=5 \newline
a^5+b^5+(ab)^2(a+b)=5 \to (...) -(\frac{1}{2})^2(1)=5 \to ...=5-\frac{1}{4} \to \color{Blue} a^5+b^5=\frac{19}{4} \newline
\color{Blue} (a^3+b^3)^2=(\frac{5}{2})^2 \to \color{Black} a^6+2a^3b^3+b^6=\frac{25}{4} \to ...+2(ab)^3 \to 2(-\frac{1}{2})^3=-\frac{1}{4} \newline
a^6+b^6=\frac{25}{4}+\frac{1}{4}=\frac{26}{4} \color{Blue} \to \frac{13}{2} \newline
\color{Blue} (a^5+b^5)(a^6+b^6)=\frac{19}{4}\frac{13}{2} \color{Black} \to a^{11}+b^{11}+a^5b^6+a^6b^5=\frac{247}{8} \to ...(ab)^5(a+b) \newline
a^{11}+b^{11}+(-\frac{1}{2})^5(1)) \to \color{Blue} a^{11}+b^{11}=\frac{247}{8}+\frac{1}{32}=\frac{989}{32}Eu adoraria dizer que muita coisa mudou desde meu tempo, mas a escola permaneceu a mesma. Dando aulas de reforço para uma aluna do primeiro grau, cuja escola particular usa material da Positivo, notei que, ao final de um dos capítulos, havia um QR code. Comentei isso com ela, de como eu achava interessante esse conteúdo multimídia adicional que esses materiais trazem. Ela não entendeu. Foi quando li o QR code e mostrei a ela um jogo interativo ensinando a calcular números positivos e negativos. Você tinha que ajudar uma lula a não ser devorada por um tubarão, acertando as continhas que apareciam na tela.
Antes disso, eu estava ajudando-a a abstrair com uma régua, marcando um ponto central nela e pedindo a ela para percorrer as marcas de medida conforme as equações que encontrávamos. Então, descobrimos que a mãe dela pagou quase R$3.500 por um material rico como aquele, e NENHUM professor da instituição recomendou aos alunos acessar esse material. A figura docente, do alto de sua insegurança em forma de deferência, parece ter escondido esta faceta do material dos próprios alunos, insistindo naquela mentalidade burguesa de que as pessoas precisam sofrer para aprenderem. Triste. Uma educação bancária limitadíssima, que obriga jovens de 12 anos a lerem autos do Gil Vicente. Dá para ser mais anacrônico do que isso?
O conhecimento deve ser divertido ou, no mínimo, interessante. Se não é nenhuma dessas coisas, tem algo errado no método do professor. Somos vendedores de um produto que todos consideram inútil até precisarem. Como planos de saúde. Como o ENEM empobrece a experiência do aprendizado…
E se acha que essa educação baseada em metas se restringe à educação básica, devo informá-lo de uma ferramenta do demônio chamada de currículo Lattes. Felizmente, nem todas as instituições cedem a esse status quo da comunidade científica, como esta universidade suíça mencionada na imagem abaixo:

Se somos condicionados a aprender pelo interesse, como esperar algo diferente da educação superior para frente?
Talvez isso seja coisa de quem trabalha tempo demais em uma área, como um açougueiro que vira vegano ou educador físico que fuma. Mas simplesmente não consigo ver relevância na maioria dos trabalhos acadêmicos que reviso. Sempre me deparo com uma escrita engessada, cercada de redundâncias e inseguranças. Não me leve a mal, eu respeito o esforço intelectual de meus clientes para produzir conhecimento, mas o currículo Lattes arruína tudo. O conhecimento, como outros relacionamentos desta vida, vem com o tempo, e não é um órgão do governo cobrando meta que vai mudar isso. Aquela coisa no imaginário coletivo, da relação mestre-discípulo tão cara ao Oriente, não existe na academia. Fazer uma pós-graduação é ter um orientador que é uma espécie de Seu Miyagi às avessas. Em vez de ensinar caratê, ele te manda encerar toda a frota dele, e ainda reclama se você se atrasar por o doidinho do bairro ter batido em você no caminho. Me gabo de fazer o trabalho do orientador, em muitos aspectos. E infelizmente não exagero: vários somem do mapa e ficam dando entrevistinha na TV universitária ou fazendo estágio pós-doutoral em vez de trabalhar.
Quem nunca experimentou abandono afetivo, vai começar a fazê-lo ao ter um orientador. Notas boas, bom comportamento em sala, prazos cumpridos? Nada parece o bastante para se obter validação. Tudo que importa é artigo. O conhecimento possui diversas competências, e o sistema cobra apenas uma. Docência, coordenação de projetos, produção de artigos que ninguém lerá, aplicação na sociedade do que se aprende na academia… tantas possibilidades, e só uma é considerada. Um narcisismo intelectual que te faz sentir sempre culpado e atrasado para cumprir metas, independentemente de seu desempenho e pontualidade nelas. Um ghosting legitimado pelo discurso hipócrita de o estudante precisar ganhar autonomia.
Seguem abaixo algumas observações rotineiras em minhas revisões. Ressalto que as elenco aqui sem nenhuma intenção de menosprezar o trabalho das pessoas, mas sim de apontar coisas que um orientador mais dedicado poderia aconselhar:
The research had limitations regarding the return of the questionnaire administered. Therefore, the number of respondents may not be representative enough to extrapolate the results to the entire population of companies providing accounting services. A larger sample could provide more robust and reliable results.
A colocação acima é um clássico. Não precisa avisar isso ao leitor. Mesmo discursos que são entendidos como imutáveis, como os religiosos, são passíveis de análises e discussões. Nada é acabado nesse mundo, muito menos o conhecimento. E sim, já revisei trabalhos cujo autor citava obras religiosas. Preocupante.