As descobertas foram obtidas exportando as 50 últimas partidas que joguei até 8 de outubro de 2024, e analisadas no Lucas Chess. Não deve ter nada de muito novo aqui para um jogador comum, mas qualquer narrativa fica interessante com dados.

Com as brancas, usei mais a abertura vienesa, que consiste em mover o peão para E4, ao passo que o adversário move o peão para E5 e as brancas movem o cavalo do flanco esquerdo para C3. Treinando aberturas no mesmo aplicativo, esta abertura tem se mostrado bem eficiente por dificultar a aplicação do mate pastor por parte do adversário. Após E5, se o adversário mover a dama para H4, as brancas podem mover o cavalo para F3. Se não der tempo, uma alternativa drástica é a de proteger o rei com sua própria dama, o que muitas vezes funciona como mecanismo de dissuasão, quando não dá tempo de mover o cavalo do flanco direito.
A Réti começa movendo o cavalo do flanco direito para F3, com preto indo para D5 com o peão e as brancas movendo o peão para E4. Embora eu tenha usado pouco em minhas partidas, o índice de vitórias é alto, e com certeza vou cogitar aplicá-lo mais. Quanto à abertura dos 4 cavalos, ambos oponentes jogam seus peões para o centro, e se as brancas movem o cavalo para atacar um peão, as pretas movem o cavalo que não o faz, as brancas fazem o mesmo, e por fim o cavalo das pretas ataca o peão das brancas. Opção para estudar o adversário e ganhar tempo.
A defesa Petrov, variante dos 3 cavalos, faz algo um pouco diferente. Após os dois peões no centro, os cavalos de ambos os lados se movem para atacar os respectivos peões, mas no próximo movimento das brancas, o terceiro, o cavalo da esquerda é movimentado sem atacar. A Vienna game começa com os peões no centro e, após as brancas moverem o cavalo para C3, as brancas, em vez de usar a mesma peça, optam pelo bispo C5, na mesma coluna das brancas, atacando o cavalo das brancas pela diagonal. O índice de derrotas é alto para meu perfil.
A defesa Alekhine foi usada poucas vezes contra mim, mas pode ser uma alternativa conforme eu ganhe mais experiência e presuma que um adversário é mais astuto. E daqui para frente, todas as aberturas foram usadas apenas uma vez, em um universo das 50 últimas partidas minhas. A abertura dos 3 cavalos é parecida com a abertura dos 4 cavalos, basta desconsiderar o último movimento, quando o cavalo das pretas ataca o peão das brancas. Possui índice de vitória muito bom. A defesa Benoni antiga, feita exclusivamente com peões, é formada por 1.e4 e6 2.d4 c5 3.d5 . Boa para as brancas ocuparem o centro e estudar o adversário. Se, após 3.d5, as pretas capturarem o peão, a coluna das brancas fica aberta e ideias de xeque podem surgir. Também possui índice bom de vitória. A defesa Robatsch moderna, por outro lado, se mostrou péssima para as brancas, sem vitórias registradas. Ao mover g6, as pretas não permitem que as brancas ataquem a torre na rodada seguinte e reforçam a diagonal do rei. O mesmo índice ruim se apresentou para a Defesa francesa: cavalo branco, embora possa ser usada para dificultar a aplicação do mate pastor por parte do adversário, e para a Defesa Pirc: gambito de Roscher. Formada por 1.e4 d6 2.d4 Nf6 3.Nf3, deixa a diagonal esquerda do rei das pretas exposta. Com uma boa estratégia, pode ser uma fraqueza interessante a ser exposta pelas brancas.
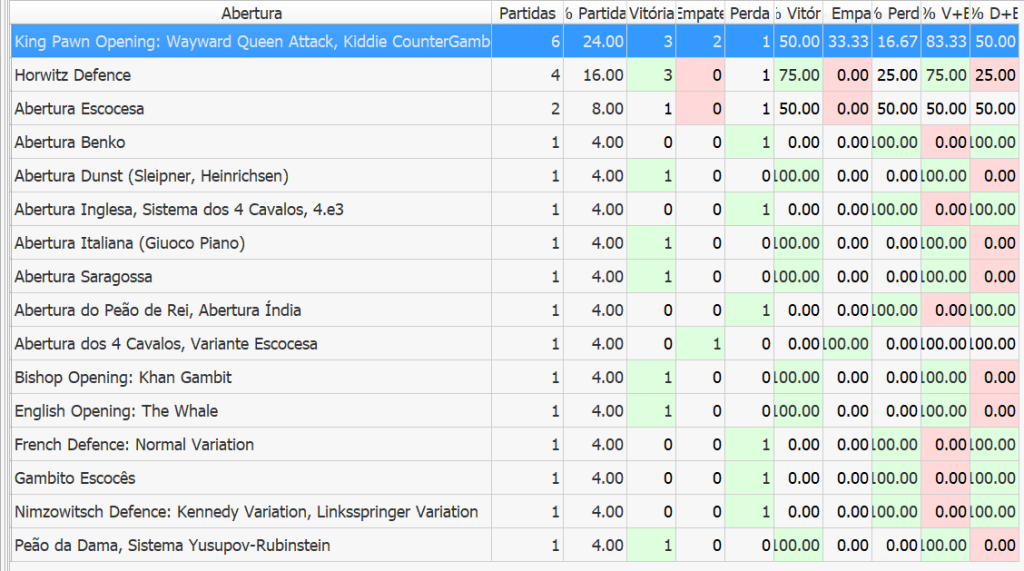
Quanto às aberturas em que eu joguei com as peças negras, os três primeiros colocados concentram a mesma quantidade de jogos que os próximos 13 colocados.
Quem sabe faz ao vivo
E isso não é meu caso, pelo menos nessas partidas que quero esquecer. O Lucas Chess gera gifs das partidas, e vou comentar algumas delas.
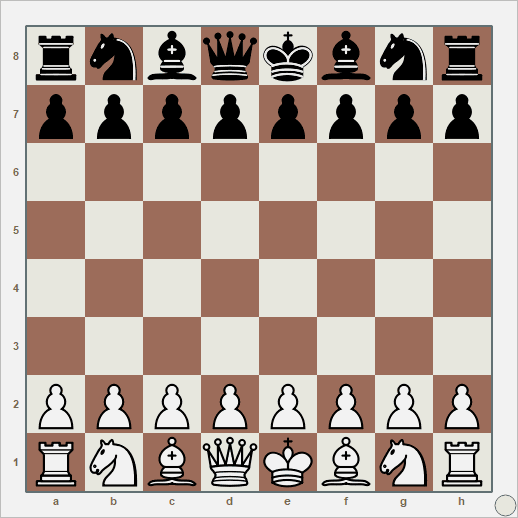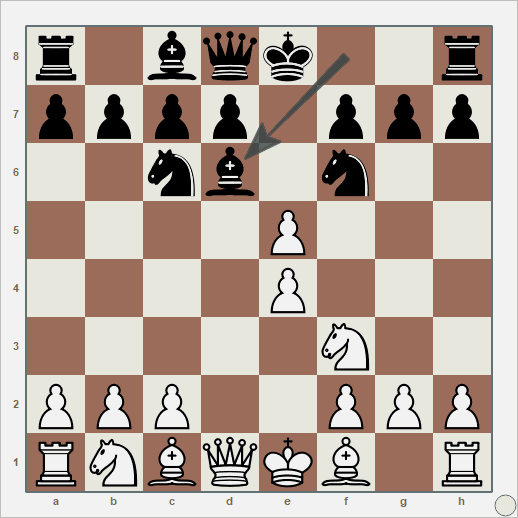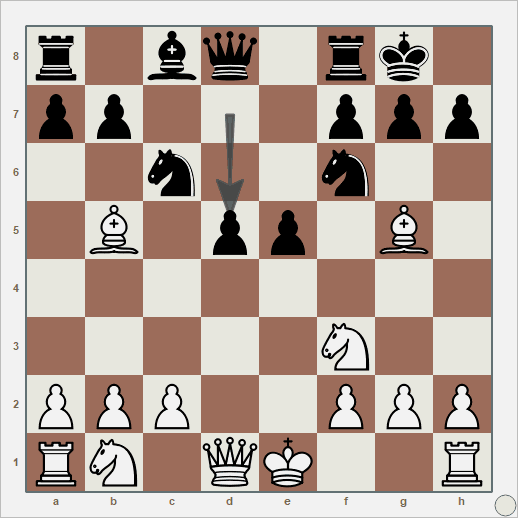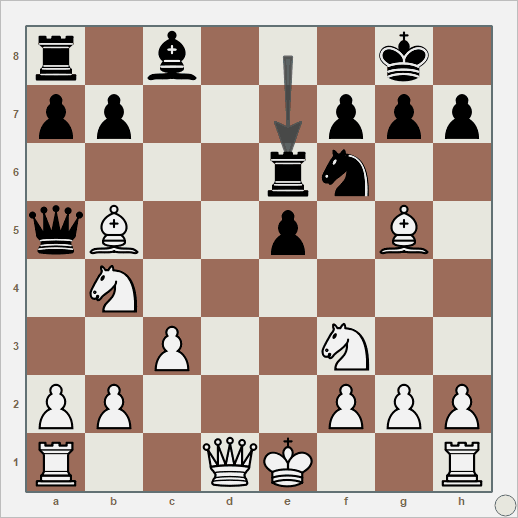
Nesta partida aqui, com abertura escocesa, eu tinha tudo para perder, mas o oponente abandonou. Joguei de pretas. Houve um momento de virada que eu não aproveitei: no lance 10, quando as brancas capturam meu peão em D5, a barra de análise dispara a favor das pretas. Era só capturar com a dama, colocando-a no centro, e perdi essa chance. Como um artilheiro superestimado no Brasileirão. Acho que, como iniciante, ainda tenho o jogo muito reativo: assim que vejo uma peça inimiga próxima à minha, meu impulso inicial é capturá-la ou fugir dela. E sempre precisamos olhar para cima.
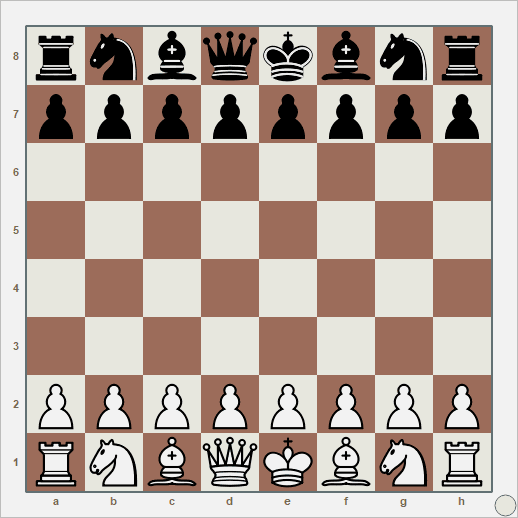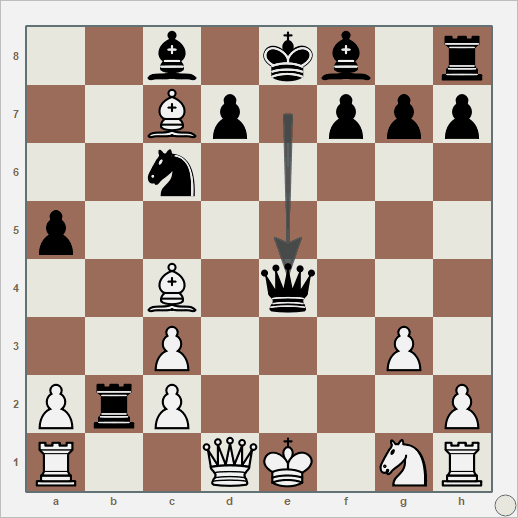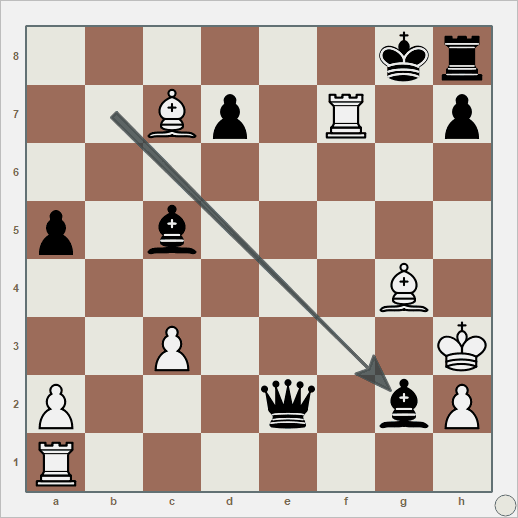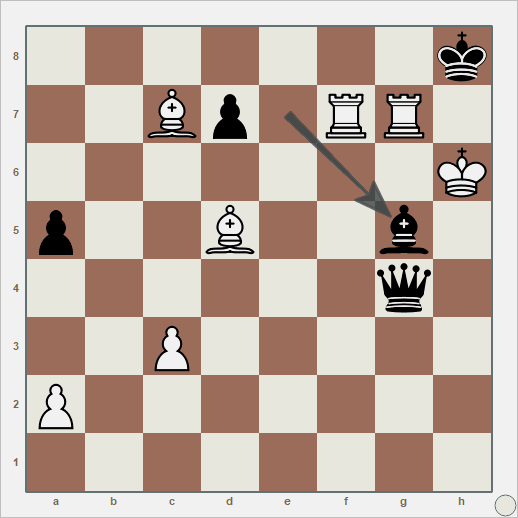
Com abertura em defesa Alekhine, a próxima partida é mais pavorosa ainda, mas os erros crassos foram dos dois lados: o emocional acabou embaralhando o jogo de ambos. São tantos erros que precisei anotar para não errar. Alguns dos piores são: Lance 8, bispo em F4, onde dei de bandeja meu cavalo. Lance 13 com XC7, onde avanço com meu bispo contra a fileira do adversário, sem peça para me cobrir. Lance 19, com XF7+, esse sendo meu, um erro que acumula com o do lance 13: tenho dois bispos na fileira adversária, e não consigo fazer nada com eles. Lance 21, com adversário movendo a dama para F5+. Perdi a oportunidade de capturá-la com minha torre em F1. Precisamos também olhar para baixo. Lance 31, com adversário movendo XH2+. Aqui, não capturei a dama com o bispo. Sim, aquele que ficou descansando na fileira inimiga. Essa dama parece um bagre ensaboado, mas eu assumo meus erros por ter arrastado um jogo ganho por tortuosas 42 rodadas.
Em algumas ocasiões, mesmo errando bastante, apliquei xeque-mate. O jogo a seguir pode ser lido no chesstempo, no Lucas chess e outros lugares. Neste jogo, repare o que o adversário fez na rodada 11: [Opening “Abertura Vienesa”]
[ECO “C25”][Result “1-0”] 1.e4 e5 2.Nc3 Qh4 3.Nf3 Qe7 4.d4 exd4 5.Nxd4 Nc6 6.Bc4 Qd6 7.O-O Nxd4 8.Re1 Qc5 9.Be3 Qxc4 10.Nd5 Nxc2 11.Qc1 Qxe4 12.Nxc7+ Kd8 13.Bg5+ Be7 14.Rxe4 Kxc7 15.Qxc2+ Kd8 16.Bxe7+ Nxe7 17.Qe2 Nc6 18.Re7 Nxe7 19.Rc1 Re8 20.Qc4 d6 21.Qc7#
Aqui, o oponente, de pretas, estava indo bem, sem grandes destaques, tendo condições de dar xeque e preparar o mate. Em vez disso, ele perdeu tempo capturando um peão solitário no centro. Como assim? Mesmo tendo meu cavalo capturado de bobeira pelo rei no lance 14, aí tudo se perde para o adversário, com o rei completamente exposto e quatro peças de ataque presas, sem poder apoiá-lo. Mesmo assim, eu quase estraguei tudo, e salvei minha vitória com a dama invadindo a fileira adversária.
E depois de ter torturado vocês com essas capivaradas, encerro com uma pintura: na partida Niemann-Maze, de 2020, o primeiro vence a partida contra o Grande Mestre sem capturar uma única peça. Uma aula de jogo posicional, de como não se expor mais do que o necessário, de como ganhar tempo. Subjugar o adversário com um garfo na hora certa pode ser mais satisfatório do que um mate.